Enoncé

\[ \forall f\in \mathcal{C}_{[a,b]}^1, \quad \exists c, \quad f'(c) = {f(b)-f(a) \over b-a} \]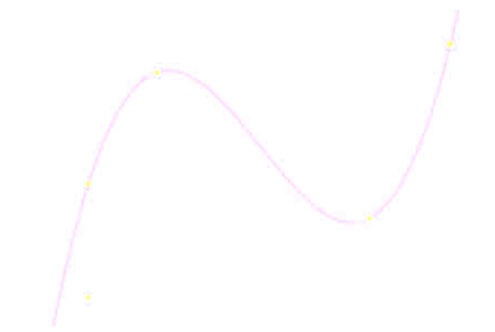

Explication

Pour toute fonction continue et dérivable sur \(]a,b[\), il existe une valeur \(c \in ]a,b[\) tel que \(f'(c) = {f(b)-f(a) \over b-a}\). Autrement dit, il existe \(c\) tel que \(f(a) - f(b) = f'(c)(a-b)\).

Inégalité des accroissements finis.

Si il existe \(m\) et \(M\) tel que, sur \(]a,b[\), \(m < f'(x) < M\), alors :
\[ m(b-a) < f(b)-f(a) < M(b-a) \]

Théorème de Rolle

C'est un cas particulier du théorème des accroissements finis pour lequel \(f(a) = f(b)\). Il existe donc \(c\) tel que \(f'(c) = 0\)